In this post I'll be looking at an F# ASP.NET Core web app and a technique for ensuring correctness when taking a contract-first approach with OpenAPI, using property based testing with Expecto and FsCheck. There's a lot to unpack there, so bear with me!

The Problem

When building a web API with Giraffe and F#, one thing that differs from MVC is you don't get an OpenAPI spec file generated automatically via tools such as NSwag, or Swashbuckle (this is being investigated in Giraffe, but I digress). This means that if we have our own OpenAPI spec file created by hand and go contract-first, we could accidentally drift our implementation from what we have specified in our OpenAPI file. If we generate an API client from our OpenAPI spec then this drifting would result in errors.

A good solution to this, and probably good practice anyway, would be to create some behavioural tests using that API client against the built web app, to make sure everything functions as expected and we get no exceptions.

A problem we now have is that the process outlined above is manual, and requires discipline. We could use code coverage to try to systematically enforce it, but there are no guarantees. In this post I will outline a way to enforce consistency between the response types which we serialize in our web app, and our OpenAPI spec file.

The OpenAPI Spec

openapi: 3.0.1
info:
  title: GiraffeDemo
  version: 1.0.0
paths:
  /student:
    get:
      responses:
        200:
          description: successful operation
          content:
            application/json:
              schema:
                $ref: '#/components/schemas/Student'
components:
  schemas:
    Student:
      type: object
      properties:
        id:
          type: integer
          format: int64
        name:
          type: string
          nullable: true
        age:
          type: integer
          format: int32
        status:
          type: string
          enum: [Active, Inactive]
        courses:
          type: array
          items:
            $ref: '#/components/schemas/Course'
      required:
        - id
        - name
        - age
        - stats
        - course
    Course:
      type: object
      properties:
        title:
          type: string
          nullable: true
        description:
          type: string
          nullable: true
        credits:
          type: integer
          format: int32
          nullable: true
        enrolmentDate:
          type: string
          format: date-time
      required:
        - title
        - enrolmentDate

We have a single route defined for GET /student, it returns some JSON that uses arrays, strings, ints, date-times, optional values, nullable values and enums.

Our Web API

module GiraffeDemo.Server.App

open System
open Microsoft.AspNetCore
open Microsoft.AspNetCore.Builder
open Microsoft.AspNetCore.Hosting
open Microsoft.Extensions.DependencyInjection
open Giraffe
open Giraffe.Serialization
open Newtonsoft.Json
open Serialization
open System.Text.Json
open System.Text.Json.Serialization

type Student =
    { Id      : int
      Name    : string
      Age     : int
      Status  : StudentStatus
      Courses : List<Course>
    }
and Course =
    { Title         : string
      EnrolmentDate : DateTime }
and StudentStatus =
    | Active
    | Inactive

let studentHandler : HttpHandler =
    fun next ctx ->
        json { Id      = 643
               Name    = "Stuart Lang"
               Age     = 33
               Status  = Active
               Courses = [
                   { Title         = "Course A"
                     EnrolmentDate = DateTime.UtcNow }
                   { Title         = "Course B"
                     EnrolmentDate = DateTime.UtcNow } ]
        } next ctx

let webApp =
    choose [
        route "/student" >=> GET >=> studentHandler
        RequestErrors.notFound (text "Not Found") ]

let configureApp (app : IApplicationBuilder) =
    app.UseGiraffe webApp

let configureServices (services : IServiceCollection) =
    services.AddGiraffe() |> ignore
    let options = JsonSerializerOptions(IgnoreNullValues = true, PropertyNamingPolicy = JsonNamingPolicy.CamelCase)
    options.Converters.Add(JsonFSharpConverter(JsonUnionEncoding.FSharpLuLike))
    services.AddSingleton<IJsonSerializer>(SystemTextJsonSerializer(options)) |> ignore

[<EntryPoint>]
let main _ =
    WebHost.CreateDefaultBuilder()
        .Configure(configureApp)
        .ConfigureServices(configureServices)
        .Build().Run()
    0

Here's our web app which returns a hardcoded response. Things to note:

  • It's lovely, it's F# & Giraffe.
  • I've swapped out the default serialization (Json.NET) for System.Text.Json and the awesome FSharp.SystemTextJson.
  • The OpenAPI Student schema is easily modelled with F# types.

The API Client

In order to ensure the OpenAPI spec and the Student type in the F# code do not drift, I will create a typed HttpClient so that I have some model types I can use in my tests later. I have a post on this topic here: Generating a Typed Client for use with HttpClientFactory using NSwag.

I won't repeat myself, there are only two things of interest to note over and above the blog post:

  • Rather than swagger.json, I'm using the OpenApi 3 spec shown earlier in this post named openapi.yaml
  • I have added logic to the .csproj file to cache the generated code, so that code generation only happens when nswag.config or openapi.yaml changes. This means referencing it from test projects is much less painful as we can rebuild as needed with no waiting.

Testing

Now we have 2 classes that represent Student defined in the OpenAPI spec file; the client one that was generated, and the web app F# type we defined.

I could write a unit test that serializes an arbitrary web app Student and deserializes it with a client generated Student. Json.NET has a feature that is handy here, and that's MissingMemberHandling = MissingMemberHandling.Error—with this setting if we have a property in the serialized JSON (and therefore in the web app) and missing from the client type (and therefore the OpenAPI spec file), then it will throw an exception.

Compatibility Checking Code

module GiraffeDemo.ContractTests.Utils

open Newtonsoft.Json
open System.Text.Json
open System.Text.Json.Serialization

let checkCompatiblityWith<'T> input =
    let options = JsonSerializerOptions(IgnoreNullValues = false, PropertyNamingPolicy = JsonNamingPolicy.CamelCase)
    options.Converters.Add(JsonFSharpConverter(JsonUnionEncoding.FSharpLuLike))

    let json = JsonSerializer.Serialize(input, options)

    let deserializeSettings = JsonSerializerSettings(NullValueHandling = NullValueHandling.Include, MissingMemberHandling = MissingMemberHandling.Error)
    JsonConvert.DeserializeObject<'T>(json, deserializeSettings) |> ignore

This function just takes an input object, it will serialize it then deserialize it using the generic type 'T.

Property Based Testing

The problem is that we'd need to create a lot of arbitrary instances of Student to prove that we can safely round-trip all cases, for example we'd want to experiment with:

  • Empty lists and non-empty lists (which will be serialized to arrays)
  • Options<T> - make sure that Some "Text" works, and None.
  • Interesting values - unusual characters in strings, negative numbers, etc...

This is where property based testing comes in! Property based testing lets us define an invariant test that takes a number of inputs, and it will create arbitrary inputs automatically, it will deliberately make the inputs interesting, and if the test fails it will simplify the input to its simplest form and display it.

Now let's write the property tests using Expecto and FsCheck.

module GiraffeDemo.ContractTests.Tests.Responses

open Expecto
open GiraffeDemo.ContractTests.Utils
open GiraffeDemo

// These tests will fail if we have added or changed the shape of the API response that has not been reflected in the OpenAPI file
[<Tests>]
let tests =
    testList "Check Response Types" [
        testProperty "Check Student" <| fun (response:Server.App.Student) ->
            response |> checkCompatiblityWith<Client.Student>
    ]

And that's it! Any additional response types we add to our web app will be just 2 more lines of code. Here is the output when running it:

Successful run!

Don't be fooled by the output here, although it says it has run 1 test, it has run the scenario 100 times, with uniquely generated values of response. Even though the values are generated, the logic is completely deterministic, so we always get the same results.

Now let's prove it's working—I have added a property to our server type named serverBlah:

Adding property to server type

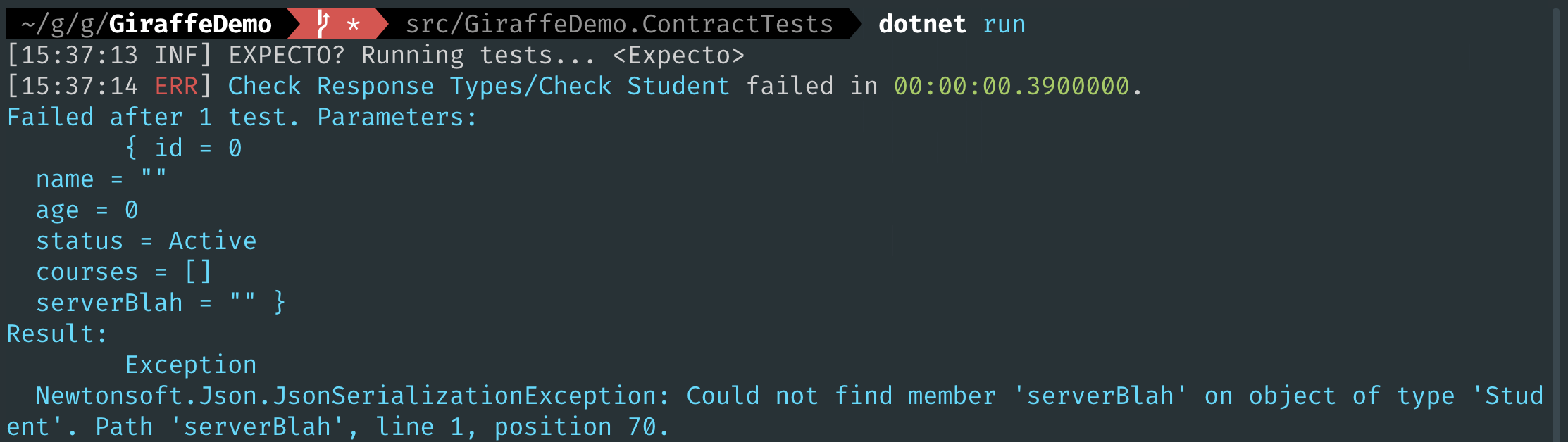
So it has failed as expected. When it fails, FsCheck will go through a process of "shrinking" the input so that we get the simplest input that causes this failure.

Now I have reverted this change, and have added a required property to the OpenAPI spec file named openapiBlah:

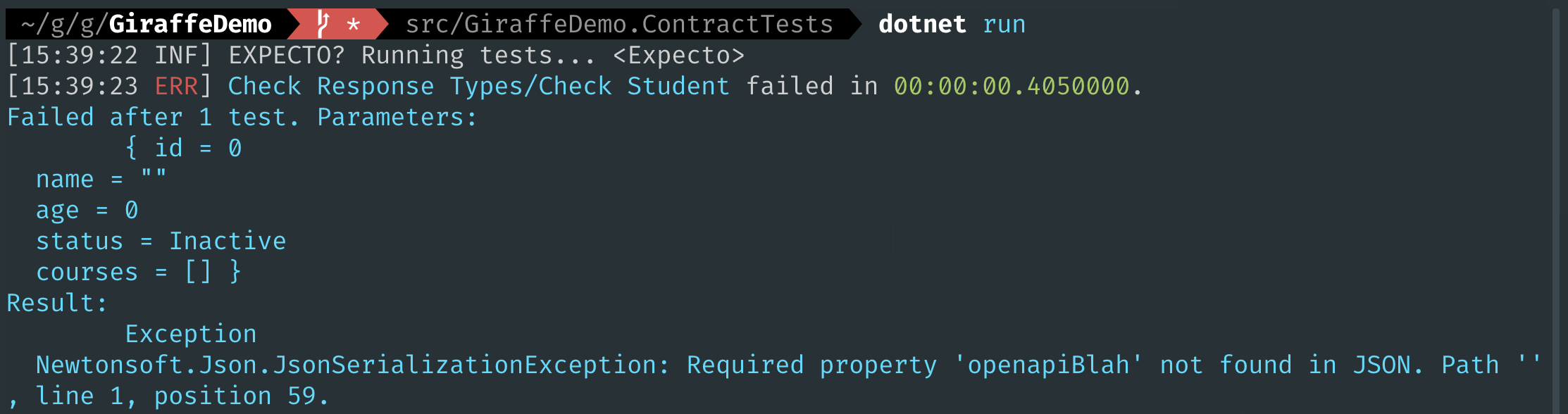
Adding a property to OpenAPI spec file

Awesome 🙂

Wrapping up

This technique doesn't cover all bases as we are only checking the response types are aligned, rather than anything else, for example request paths or input parameters. However, I hope the idea behind this was interesting and useful—that you can use property based testing to automate compatibility testings.

Here is what our finished solution looks like:

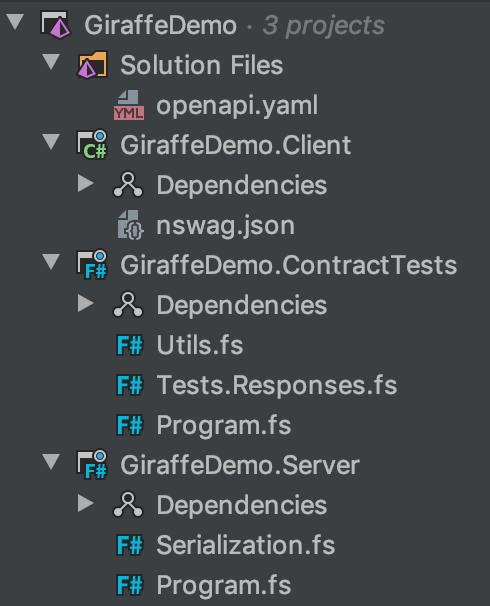
You can look through all the code here:

slang25/GiraffeDemo
Contribute to slang25/GiraffeDemo development by creating an account on GitHub.
GitHubslang25